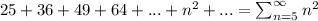Question

Write the sum using summation notation, assuming the suggested pattern continues.

25 + 36 + 49 + 64 + ... + n2 + ...

Answer 1

The sum using summation notation, assuming the suggested pattern continues is :

`25 + 36 + 49 + 64 + ... + n^2 + ...=\sum_(n=5)^(\infty) n^2`

Explanation:

We are given a series of numbers as

25 + 36 + 49 + 64 + ... + n^2 + ...

To write the sum using summation notation means we need to express this series in terms of a general n such that there is a whole summation expressing this series.

Here we see that each of the numbers could be expressed as follows:

`25=5^2\\\\36=6^2\\\\49=7^2\\\\64=8^2`

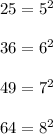
and so on.

i.e. the series starts by taking the square of 5 then of 6 then 7 and so on.

and the series goes to infinity.

Hence, the summation notation will be given by:

`25 + 36 + 49 + 64 + ... + n^2 + ...=\sum_(n=5)^(\infty) n^2`

Answer 2

`\sum_(n=5)^(\infty)n^2`

Explanation:

The pattern given is:

25+36+49+64+...+n^2+...

The pattern can be written as

(5)^2+(6)^2+(7)^2+(8)^2+.....+n^2+....

The series is started with 5 and it continues up to infinity.

The summation notation for the given series is:

`\sum_(n=5)^(\infty) n^2`

n= 1 and goes up to infinity and the series is made up of taking square of n,