Question

9. An RSA cryptosystem has modulus n 391, which is a product of the primes 23 and 17. Which of the following is suitable as an encoding key e? (a) 163 (b) 353 (c) 351 (d) 277 (e) none of these. 10. Which of the following polynomials p(x) is complete over Zalr? (a) z4+1 (e) none of these

Answer 1

163

Explanation:

So n=391.

This means p=23 and q=17 where p*q=n.

`\lambda (391)=lcm(23-1,17-1)=lcm(22,16)=2*8*11=16*11=176.`

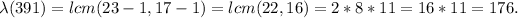
We want to choose e so that e is between 1 and 176 and the gcd(e,176)=1.

There is only one number in your list that is between 1 and 176... Hopefully the gcd(163,176)=1.

It does. See notes below for checking it:

176=2(88)=2(4*22)=2(2)(2)(2)(11)

None of the prime factors of 176 divide 163 so we are good.

The answer is 163.