Question

The average time required to complete an accounting test has been determined to be 55 minutes. Assuming that times required to take tests are exponentially distributed, how many students from a class of 30 should be able to complete the test in between 45 and 60 minutes?

Answer 1

Answer: 3

Explanation:

Given : The average time required to complete an accounting test :
`\lambda = 55 \text{ minutes}=0.9167\text{ hour}`

Interval = (45, 60) minutes

In hour : Interval = (0.75, 1)

The cumulative distribution function for exponential function is given by :-

`F(x)=1- e^(-\lambda x)`

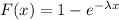
For
`\lambda =0.9167\text{ hour}`

`P(X\leq1)=1- e^(-(0.9167) (1))=0.6002`

`P(X\leq0.75)=1- e^(-(0.9167)(0.75))=0.4972`

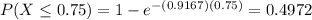
Then ,

`P(0.75<x<1)=P(X\leq1)-P(X\leq0.75)\\\\=0.6002-0.4972=0.103`

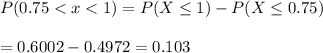
Now, the number of students from a class of 30 should be able to complete the test in between 45 and 60 minutes =

`0.103*30=3.09\approx3`

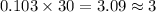
Hence, the number of students should be able to complete the test in between 45 and 60 minutes =3