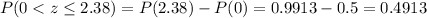Question

Suppose the sediment density (g/cm) of a randomly selected specimen from a certain region is normally distributed with mean 2.61 and standard deviation 0.82. (a) If a random sample of 25 specimens is selected, what is the probability that the sample average sediment density is at most 3.00? Between 2.61 and 3.00

Answer 1

Answer: The probability that the sample average sediment density is at most 3.00 = 0.9913

The probability that the sample average sediment density is between 2.61 and 3.00 = 0.4913

Step-by-step explanation:

Given : Mean :
`\mu=2.61`

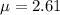
Standard deviation :
`\sigma =0.82`

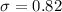
Sample size :
`n=25`

The value of z-score is given by :-

`z=(x-\mu)/((\sigma)/(√(n)))`

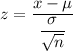
a) For x= 3.00

`z=(3.00-2.61)/((0.82)/(√(25)))=2.38`

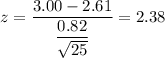
The p-value :
`P(z\leq2.38)=0.9913`

b) For x= 2.61

`z=(2.61-2.61)/((0.82)/(√(25)))=0`

The p-value :
`P(0<z\leq2.38)=P(2.38)-P(0)=0.9913-0.5=0.4913`