Question

Find the coefficient of x3 y4 in the expansion of ( x+2y )^7.

Answer 1

The coefficient of x³y⁴ in the expansion of ( x+2y)⁷ is 560.

Step-by-step explanation:

The given expression is

`(x+2y)^7`

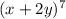
According to binomial expansion,

`(a+b)^n=^nC_0a^nb^0+^nC_1a^(n-1)b^1+...+^nC_(n-1)a^1b^(n-1)+^nC_0a^0b^n`

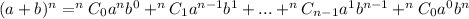
The r+1th term of the expansion is

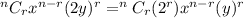`^nC_rx^(n-r)(2y)^r=^nC_r(2^r)x^(n-r)(y)^r` ... (1)

In the term x³y⁴ the power of x is 3 and the power of y is 4. It means the value of r is 4 and the value n-r is 3.

`n-r=3`

`n-4=3\Rightarrow n=7`

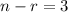
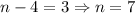
Put n=7 and r=4 in equation (1)

`^7C_4(2^4)x^(7-4)(y)^4`

`(7!)/(4!(7-4)!)(16)x^3y^4`

`(7* 6* 5* 4!)/(4!(3)!)(16)x^3y^4`

`560x^3y^4`

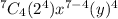
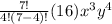
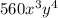
Therefore the coefficient of x³y⁴ in the expansion of ( x+2y)⁷ is 560.