Question

Find all polar coordinates of point P where P = ordered pair 1 comma pi divided by 3.

Answer 1

(1, π/3 +2kπ), (-1, 4π/3 +2kπ) . . . where k is any integer

Explanation:

Adding any multiple of 2π to the angle results in the same point in polar coordinates.

Adding 180° (π radians) to the point effectively negates the magnitude. As above, adding any multiple of 2π to this representation is also the same point in polar coordinates.

There are an infinite number of ways the coordinates can be written.

Answer 2

All the polar coordinates of point P are
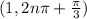`(1,2n\pi+(\pi)/(3))` and
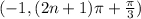`(-1,(2n+1)\pi+(\pi)/(3))`, where n is an integer.

Explanation:

The given point is

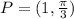`P=(1,(\pi)/(3))` .... (1)

If a point is defined as

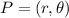`P=(r,\theta)` .... (2)

then the polar coordinates of point P is defined as

`(r,\theta)=(r,2n\pi+\theta)`

`(r,\theta)=(-r,(2n+1)\pi+\theta)`

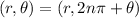
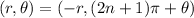
where, n is an integer and θ is in radian.

From (1) and (2) we get

`r=1, \theta=(\pi)/(3)`

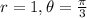
So, the polar coordinates of point P are

`(r,\theta)=(1,2n\pi+(\pi)/(3))`

`(r,\theta)=(-1,(2n+1)\pi+(\pi)/(3))`

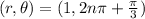
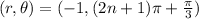
Therefore all the polar coordinates of point P are
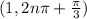`(1,2n\pi+(\pi)/(3))` and
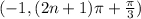`(-1,(2n+1)\pi+(\pi)/(3))`, where n is an integer.