Question

You are told that a sample of size 225 the mean is 48.5 and the standard deviation is 1.8 the study is reported with 90% confidence level explain how to determine if 48.8 is within the confidence interval

Answer 1

sample answer

Explanation:

To find the margin of error, multiply the z-score by the standard deviation, then divide by the square root of the sample size.

The z*-score for a 90% confidence level is 1.645.

The margin of error is 0.20.

The confidence interval is 48.3 to 48.7.

48.8 is not within the confidence interval.

Answer 2

Answer with explanation:

Size of the sample = n =225

Mean[\text] \mu[/text]=48.5

Standard deviation [\text] \sigma[/text]= 1.8

`Z_{90 \text{Percent}}=Z_(0.09)=0.5359\\\\Z_(score)=\frac{\Bar X -\mu}{\frac{\sigma}{\sqrt{\text{Sample size}}}}\\\\0.5359=(\Bar X -48.5)/((1.8)/(√(225)))\\\\0.5359=15 * (\Bar X -48.5)/(1.8)\\\\0.5359 * 1.8=15 * (\Bar X -48.5)\\\\0.97=15 \Bar X-727.5\\\\727.5+0.97=15 \Bar X\\\\728.47=15 \Bar X\\\\ \Bar X=(728.47)/(15)\\\\\Bar X=48.57`

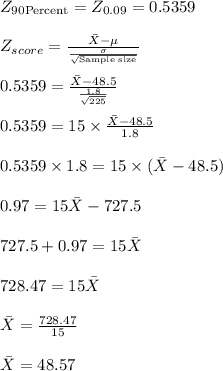
→Given Confidence Interval of Mean =48.8

→Calculated Mean of Sample =48.57 < 48.8

So, the value of Sample mean lies within the confidence interval.