Question

If tan^3(theta) -1/tan(theta)-1 - sec^2(theta) + 1 = 0 find cot(theta)

Answer 1

`\tan^3\theta-\frac1{\tan\theta-1}-\sec^2\theta+1=0`

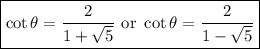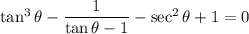
Recall that
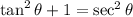`\tan^2\theta+1=\sec^2\theta`, so we can write everything in terms of
`\tan\theta`:

`\tan^3\theta-\frac1{\tan\theta-1}-\tan^2\theta=0`

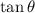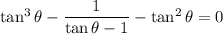
Let
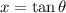`x=\tan\theta`, so that

`x^3-\frac1{x-1}-x^2=0`

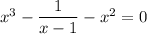
With some rewriting we get

`x^3-x^2-\frac1{x-1}=0`

`x^2(x-1)-\frac1{x-1}=0`

`(x^2(x-1)^2-1)/(x-1)=0`

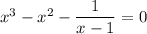
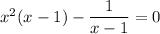
Clearly we cannot have
`x=1`, or
`\tan\theta=1`.

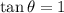The numerator determines when the expression on the left reduces to 0:

`x^2(x-1)^2-1=0`

`x^2(x-1)^2=1`

`√(x^2(x-1)^2)=\sqrt1`

`|x(x-1)|=1`

`x(x-1)=1\text{ or }x(x-1)=-1`

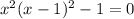
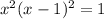
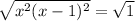
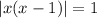
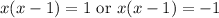
Completing the square gives

`x(x-1)=x^2-x=x^2-x+\frac14-\frac14=\left(x-\frac12\right)^2-\frac14`

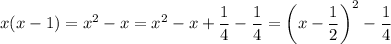
so that

`\left(x-\frac12\right)^2=\frac54\text{ or }\left(x-\frac12\right)^2=-\frac34`

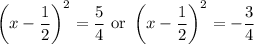
The second equation gives no real-valued solutions because squaring any real number gives a positive real number. (I'm assuming we don't care about complex solutions.) So we're left with only

`\left(x-\frac12\right)^2=\frac54`

`√(\left(x-\frac12\right)^2)=√(\frac54)`

`\left|x-\frac12\right|=\frac{\sqrt5}2`

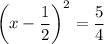
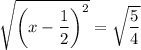
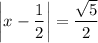
which again gives two cases,

`x-\frac12=\frac{\sqrt5}2\text{ or }x-\frac12=-\frac{\sqrt5}2`

`x=\frac{1+\sqrt5}2\text{ or }x=\frac{1-\sqrt5}2`

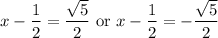
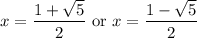
Then when
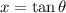`x=\tan\theta`, we can find
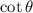`\cot\theta` by taking the reciprocal, so we get

`\boxed{\cot\theta=\frac2{1+\sqrt5}\text{ or }\cot\theta=\frac2{1-\sqrt5}}`

Answer 2

Answer: A. -1

Explanation:

Edg 2020