Question

The average annual salary for employees in a store is $50,000. It is given that the population standard deviation is $4,000. Suppose that a random sample of 70 employees will be selected from the population.What is the value of the standard error of the average annual salary? Round your answer to the nearest integer.

Answer 1

Answer: 478

Explanation:

The formula to calculate the standard error of the population mean is given by :-

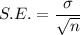`S.E.=(\sigma)/(√(n))`, where
`\sigma` is the standard deviation and 'n' is the sample size.

Given: Mean :
`\mu=$\50,000`

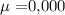
Standard deviation :
`\sigma= $\4,000`

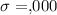
Sample size :
`n=70`

Now, the value of the standard error of the average annual salary is given by :-

`S.E.=(50000)/(√(70))=478.091443734\approx478`

Hence, the standard error of the average annual salary = 478