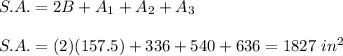Question

Find he volume and surface area of the figure. Round to the nearest one hundredth when necessary. Explain please if you can.

Answer 1

`\large\boxed{V=3780\ in^3}\\\boxed{S.A.=1827\ in^2}`

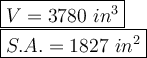
Explanation:

The formula of a volume of a prism:

`V=BH`

B - base area

H - height

In the base we have the right triangle. The formula of an area of a right triangle:

`A=((a)(b))/(2)`

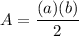
a, b - legs

We have a = 14in and b = 22.5in. Substitute:

`B=((14)(22.5))/(2)=157.5\ in^2`

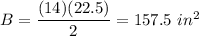
H = 24in.

Calculate the volume:

`V=(157.5)(24)=3780\ in^3`

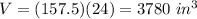
The Surface Area:

We have

(1) two right triangles with area 157.5 in²

(2) three rectangles 24 in × 14 in, 24 in × 22.5 in, 24 in × 26.5 in.

Calculate the areas of the rectangles:

`A_1=(24)(14)=336\ in^2\\\\A_2=(24)(22.5)=540\ in^2\\\\A_3=636\ in^2`

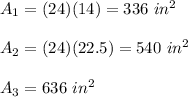
The Surface Area:

`S.A.=2B+A_1+A_2+A_3\\\\S.A.=(2)(157.5)+336+540+636=1827\ in^2`