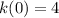Answer and Explanation:
This is a piecewise function because it is defined by more than two functions. Basically, we want to take the limit here. Recall that if a function
 approaches some value
approaches some value
 as
as
 approaches
approaches
 from both the right and the left, then the limit of
from both the right and the left, then the limit of
 exists and equals
exists and equals
 . Here we won't calculate the limit, but apply some concepts of it. So:
. Here we won't calculate the limit, but apply some concepts of it. So:
a.
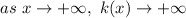
Move on the x-axis from the left to the right and you realize that as x increases y also increases without bound.
b.
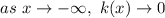
Move on the x-axis from the right to the left and you realize that as x decreases to negative values y approaches zero.
c.
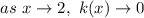
Since the function is continuous here, we can say that
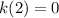
d.
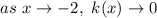
The function is discontinuous here, but
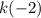 exists and equals 0 as the black hole indicates at
exists and equals 0 as the black hole indicates at
 .
.
e.
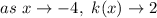
The function is also discontinuous here, but the black hole indicates that this exists at
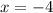 , so
, so

f.
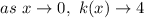
Since the function is continuous here, we can say that