Question

The mean number of flight hours for Continental Airline pilots is 49 hours per month. Assume that this mean was based on a sample of 100 Continental pilots and that the sample standard deviation was 11.5 hours. (a) Calculate the margin of error for a 95% confidence interval. (b) Calculate the upper bound for a 95% confidence interval.

Answer 1

Answer with explanation:

(a)

Mean number of flight hours for Continental Airline pilots = 49 hours per month

Total Sample Size =100

Standard Deviation =11.5 Hours

Margin of error for a 95% confidence interval

`=Z_{95 \text{Percent}}* (\sigma)/(√(n))\\\\=0.8365 * (11.5)/(√(100))\\\\=(9.61975)/(10)\\\\=0.961975\\\\=0.97(\text{Approx})`

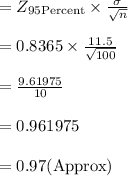
(b)

The Range of values for a 95% confidence interval

⇒ Mean number of flight + Margin of Error ≤ Confidence interval ≤ Mean number of flight - Margin of Error

⇒ 49+0.97 ≤ Confidence interval ≤ 49-0.97

⇒ 49.97 ≤ Confidence interval ≤48.03

Upper Bound = 49.97