Question

Solve the inequality and express your answer in interval notation. x^2+6x+7<0

Answer 1

The other guy is absolutely right, however

we can change his 4.41 to 3 + or - sqrt2

Explanation:

So C

Answer 2

Hello!

The answer is:

The interval notation will be: (-∞,-1.59) and (-4.41,∞+)

Why?

To solve the expression, we need to perform the following steps:

- Find the roots or zeroes of the expression:

Using the quadratic equation, we have:

`\frac{-b+-\sqrt{b^(2)-4*a*c } }{2*a}`

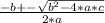
We are given the quadratic expression:

`x^(2) +6x+7`

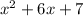
Where,

`a=1\\b=6\\c=7`

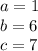
Then, substituting and calculating we have:

`\frac{-6+-\sqrt{6^(2)-4*1*7 } }{2*1}=(-6+-√(36-28 ) )/(2)\\\\(-6+-√(36-28))/(2)=(-6+-√(8))/(2)\\\\x_(1)=(-6+√(8))/(2)=(-6+2.82)/(2)=-1.59\\\\x_(2)=(-6-√(8))/(2)=(-6-2.82)/(2)=-4.41`

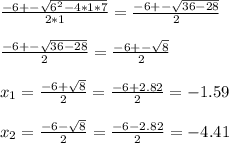
- Inequality interpretation:

Now that we already know the roots of the quadratic expression, and we can see that the parabola open upwards (positive quadratic coefficient), we can conclude that the function is less than 0 between the numbers -4.41. and -1.59

The interval notation will be:and (-∞,-1.59) and (-4.41,∞+)

Have a nice day!

Note: I have attached a picture for better understanding.