Question

If sinθ = 2/3 and θ is located in Quadrant II, then tan2θ = _____.

Answer 1

`-4 √(5)`

Explanation:

Quadrant 2 means cosine is negative.

So
`\sin(\theta)=(2)/(3) =\frac{\text{ opp }}{\text{ hyp }}`

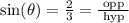
So the adjacent side is
`√(3^2-2^2)=√(9-4)=√(5)`

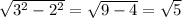
So
`\cos(\theta)=-(√(5))/(3)`

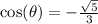
Now to find
`\tan(2 \theta)`

`\tan(2 \theta) =(2\tan(\theta))/(1-\tan^2(\theta))`

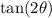
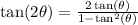
We will need
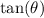`\tan(\theta)` before proceeding.

`\tan(\theta) =(\sin(\theta))/(\cos(\theta))=((2)/(3))/((-√(5))/(3))=(-2)/(√(5) )`

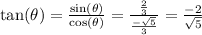
Now plug it in and the rest is algebra.

`\tan(2 \theta) =(2\tan(\theta))/(1-\tan^2(\theta)) =(2 ((-2)/(√(5)))/(1-(4)/(5))`

Now the algebra, the simplifying.... We need to get rid of the compound fraction. We will multiply top and bottom by
`5 √(5)`

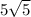
This will give us

`(-4(5))/(5 √(5)-4 √(5))`

`(-20)/(√(5))`

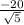
Multiply top and bottom by
`√(5)`

`(-20 √(5))/(5)`

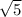
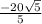
The answer reduces to

`-4 √(5)`