Question

If cosine theta equals one over six, what are the values of sin θ and tan θ?

A) sine theta equals plus or minus seven times square root of five over six, tangent theta equals plus or minus seven times square root of five

B) sine theta equals plus or minus square root of thirty-five over six, tangent theta equals negative seven times square root of five

C) sine theta equals plus or minus seven times square root of five over six, tangent theta equals negative square root of thirty five

D) sine theta equals plus or minus square root of thirty-five over six, tangent theta equals plus or minus square root of thirty five

Answer 1

Option D. sine theta equals plus or minus square root of thirty-five over six, tangent theta equals plus or minus square root of thirty five

Explanation:

we have that

`cos(\theta)=(1)/(6)`

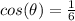
If the cosine is positive, then the angle theta lie on the first or fourth Quadrant

therefore

The sine of angle theta could be positive (I Quadrant) or negative (IV Quadrant) and the tangent of angle theta could be positive (I Quadrant) or negative (IV Quadrant)

step 1

Find
`sin(\theta)`

Remember that

`sin^(2) (\theta)+cos^(2) (\theta)=1`

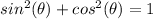
we have

`cos(\theta)=(1)/(6)`

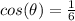
substitute

`sin^(2) (\theta)+((1)/(6))^(2)=1`

`sin^(2) (\theta)+(1)/(36)=1`

`sin^(2) (\theta)=1-(1)/(36)`

`sin^(2) (\theta)=(35)/(36)`

`sin(\theta)=(+/-)(√(35))/(6)`

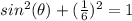
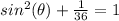
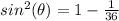
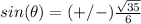
so

sine theta equals plus or minus square root of thirty-five over six

step 2

Find
`tan(\theta)`

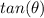
Remember that

`tan(\theta)=(sin(\theta))/(cos(\theta))`

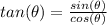
we have

`sin(\theta)=(+/-)(√(35))/(6)`

`cos(\theta)=(1)/(6)`

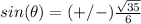
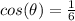
substitute

`tan(\theta)=(+/-)√(35)`

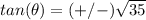
tangent theta equals plus or minus square root of thirty five