Question

Coseca/4+cota/2=cota/8-coseca/2​

Answer 1

It's not clear if this is a problem to solve or a problem to prove. Let's see where it goes.

We note the cotangent half angle formula is

`\cot x = ( 1 + \cos 2x)/(\sin 2x)`

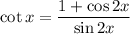
The tangent and cotangent half angle is expressible in terms of the full angle without any ambiguity, so let's set b=a/4 so a=4b.

It turns out to be true for all a (at least all a that don't make the any of the functions undefined). So it's a problem to prove.

Here's the proof. I actually did it from the bottom up, but it's better to present it this way as a proof.

We start with the cosine double angle formula:

`\cos 2b = 2\cos^2 b- 1`

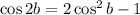
Multipy both sides by sin b:

`\sin b \cos 2b = 2 \sin b \cos^2 b - \sin b`

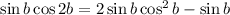
Sine double angle formula:

`\sin b \cos 2b = \sin 2b \cos b- \sin b`

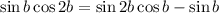
Add sin 2b to both sides:

`\sin 2b+ \sin b\cos 2b = \sin 2b + \sin 2b \cos b - \sin b`

Divide by sin b sin 2b

`(1)/(\sin b) + (\cos 2b)/(\sin 2b) = (1 + \cos b)/(\sin b) - (1)/(\sin 2b)`

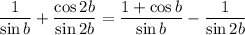
Turn to cosecants and cotangents. We use the cotangent half angle formula above.

`\csc b + \cot 2b = \cot \frac b 2 - \csc 2b`

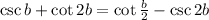
Substituting b=a/4:

`\csc \frac a 4 + \cot \frac a 2 = \cot \frac a 8 - \csc \frac a 2 \quad\checkmark`