Question

he amount of​ carbon-14 present in animal bones t years after the​ animal's death is given by ​P(t)equals=Upper P 0 e Superscript negative 0.00012097 tP0e−0.00012097t. How old is an ivory tusk that has lost 26​% of its​ carbon-14?

Answer 1

t = 2489 years

Explanation:

The equation you need for this is

`N=N_(0)e^(kt)`

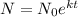
where N is the amount AFTER the decomposition, N-sub-0 is the initial amount, k is the decomposition constant and t is time in years.

If we are told that the tusk LOST 26% of its carbon-14, that means 74% of it remains from the initial 100% it had.

Filling in:

`74=100e^(-.00012097t)`

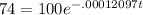
Begin by dividing both sides by 100 to get a decimal of .74:

`.74=e^(-.00012097t)`

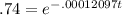
The goal is to get that t out of the exponential position in which it is currently sitting. Do this by "undoing" the e. Do THAT by taking the natural log of both sides because a natural log "undoes" an e. This is due to the fact that the base of a natural log is e.

`ln(.74)=ln(e^(-.00012097t))`

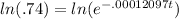
The ln and the e disappear on the right side, leaving

ln(.74) = -.00012097t

Plug ln(.74) into your calculator to get

-.3011050928 = -.00012097t

t = 2489