Question

If a distance of 75 yds is measured back from the edge of the canyon and two angles are measured , find the distance across the canyon

Angle ACB = 50°
Angle ABC=100°
a=75 yds

What does C equal?

Answer 1

Length of side
`c`:

`c = \rm AB \approx 115\; yds`.

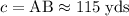The distance across the canyon is approximately

`\rm 113\;yds`.

Explanation:

• 
  `c` is the length of the side opposite to the angle
  `\rm A\hat{C} B`.
• 
  `a` is the length of the side opposite to the angle
  `\rm B\hat{A}C`.

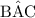Apply the law of sine:

.

In other words,

`\displaystyle c = \sin{\rm B\hat{A}C} \cdot \frac{a}{\sin{\rm A\hat{C} B}}`.

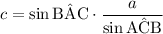However, the value of the angle
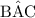`\rm B\hat{A}C` isn't given. Don't panic. The three interior angles of a triangle shall add up to 180°. Two of the three angles are given. The value of the third angle is implied.

`\rm B\hat{A}C = 180\textdegree{} - A\hat{C}B - A\hat{B}C = 30\textdegree{}`.

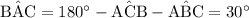Apply the law of sine to find
`c`:

`\displaystyle \begin{aligned}c &= \sin{\rm A\hat{C}B} \cdot \frac{a}{\sin{\rm B\hat{A}C}}\\ &= \sin{50\textdegree{}}\cdot \frac{\rm 75\; yds}{\sin{30\textdegree{}}}\\ &\rm = 114.907\; yds\end{aligned}`.

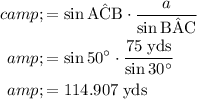Refer to the diagram. The distance across the canyon will be

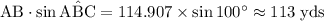`\rm AB \cdot \sin{A\hat{B}C} = 114.907* \sin{100\textdegree{}} \approx 113\;yds`.