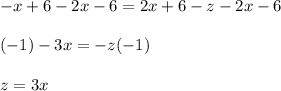Question

Leonardo wrote an equation that has an infinite number of solutions. One of the terms in Leonardo’s equation is missing, as shown below.

Answer 1

Answer:
`3x`

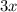
Explanation:

Let be "z" the missing term:

`-(x-1)+5=2(x+3)-z`

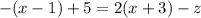
For the system to have infinite number of solutions,
`2(x+3)-z` must be equal to
`-(x-1)+5`.

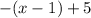Now you must solve for "z". Apply Distributive property:

`-x+1+5=2x+6-z`

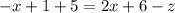
Add the like terms on the left side:

`-x+6=2x+6-z`

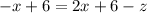
Now you need to subtract
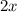`2x` and 6 from both sides of the equation and finally you can multiply both sides by -1. Then:

`-x+6-2x-6=2x+6-z-2x-6\\\\(-1)-3x=-z(-1)\\\\z=3x`

Answer 2

3x

Explanation:

-(x-1) +5 = 2(x+3) - c

C is the unknown term

Distribute the negative sign and the 2

-x+1 +5 = 2x+6 -c

Combine like terms

-x+6 = 2x +6-c

Solve for c

Add x to each side

-x+x +6 = 2x+x +6-c

6 = 3x+6 -c

Add c to each side

6+c = 3x +6 -c+c

c+6 = 3x+6

Subtract 6 from each side

c+6-6 = 3x+6-6

c = 3x

When c = 3x, the two sides of the equation are equal, and the solutions are infinite.