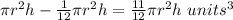Question

A cone is placed inside a cylinder. The cone has half the radius of the cylinder, but the height of each figure is the same. The cone is tilted at an angle so its peak touches the edge of the cylinder’s base. What is the volume of the space remaining in the cylinder after the cone is placed inside it?

Answer 1

11/12 Pie R^2H

Explanation:

I just took the test, good luck!

Answer 2

`(11)/(12)\pi r^(2)h\ units^(3)`

Explanation:

we know that

Te volume of the cone is equal to

`V=(1)/(3)\pi r^(2)h`

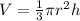
we have

`r=(r/2)\ units`

substitute

`V=(1)/(3)\pi (r/2)^(2)h`

`V=(1)/(12)\pi r^(2)h`

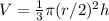
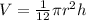
Te volume of the cylinder is equal to

`V=\pi r^(2)h`

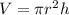
we know that

To find the volume of the space remaining in the cylinder after the cone is placed inside it, subtract the volume of the cone from the volume of cylinder

so

`\pi r^(2)h-(1)/(12)\pi r^(2)h=(11)/(12)\pi r^(2)h\ units^(3)`