The maximum rate of change occurs in the direction of the gradient vector at (1, 1, 1).
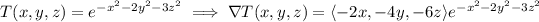
At (1, 1, 1), this has a value of
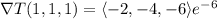
so the captain should move in the direction of the vector
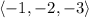 (which is a vector pointing in the same direction but scaled down by a factor of
(which is a vector pointing in the same direction but scaled down by a factor of
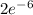 ).
).