Find the standard deviation of 21, 31, 26, 24, 28, 26

Question

asked Jun 20, 2020 139k views

1 Answer

Yanar Assaf · Answer 1 · 2020-06-24T16:24:56+0000

Given the dataset

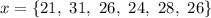
$x = \{21,\ 31,\ 26,\ 24,\ 28,\ 26\}$

We start by computing the average:

$\overline{x} = (21+31+26+24+28+26)/(6)=(156)/(6)=26$

We compute the difference bewteen each element and the average:

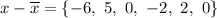
$x-\overline{x} = \{-6,\ 5,\ 0,\ -2,\ 2,\ 0\}$

We square those differences:

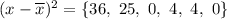
$(x-\overline{x})^2 = \{36,\ 25,\ 0,\ 4,\ 4,\ 0\}$

And take the average of those squared differences: we sum them

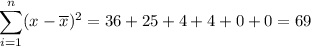
$\displaystyle \sum_(i=1)^n (x-\overline{x})^2=36+25+4+4+0+0=69$

And we divide by the number of elements:

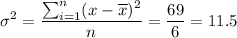
$\displaystyle \sigma^2=\frac{\sum_(i=1)^n (x-\overline{x})^2}{n} = (69)/(6) = 11.5$

Finally, we take the square root of this quantity and we have the standard deviation:

$\displaystyle\sigma = \sqrt{\frac{\sum_(i=1)^n (x-\overline{x})^2}{n}} = √(11.5)\approx 3.39$