Question

Someone help me out please

Answer 1

`6√(2) \: units`

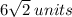
Step-by-step explanation

This is an isosceles right triangle.

The two legs of an isosceles right triangle are equal, hence each of them is 6 units each.

Let h be the hypotenuse, then from the Pythagoras Theorem,

`{h}^(2) = {6}^(2) + {6}^(2)`

`{h}^(2) = {6}^(2) * 2`

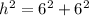
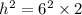
Take square root of both sides;

`{h} = \sqrt{ {6}^(2) * 2 }`

`{h}= \sqrt{ {6}^(2) } * √(2)`

`{h} = 6√(2) \: units`

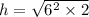
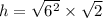
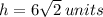
The correct answer is C

Answer 2

For this case we have to define trigonometric relations of rectangular triangles that, the cosine of an angle is given by the leg adjacent to the angle on the hypotenuse of the triangle. That is, according to the data of the figure we have:

`Cos (45) = \frac {6} {h}`

Where:

h: It's the hypotenuse

So:

`\frac {\sqrt {2}} {2} = \frac {6} {h}`

We cleared h:

`h \sqrt {2} = 6 * 2\\h \sqrt {2} = 12\\h = \frac {12} {\sqrt {2}}`

We rationalize:

`h = \frac {12 \sqrt {2}} {(\sqrt {2}) ^ 2}\\h = \frac {12 \sqrt {2}} {2}\\h = 6 \sqrt {2}`

Answer:

Option C