The vertex of the parabola below is at the point (3,2) and the point (4,6) is on the parabola. What is the equation of the parabola?

Question

asked Jan 5, 2020 139k views

2 Answers

Beatrice Zmau · Answer 1 · 2020-01-11T02:15:33+0000

Answer:

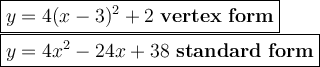
$\large\boxed{y=4(x-3)^2+2\ \bold{vertex\ form}}\\\boxed{y=4x^2-24x+38\ \bold{standard\ form}}$

Explanation:

The vertex form of a parabola:

y=a(x-h)^2+k

(h, k) - vertex

We have the vertex at (3, 2) → h = 3 and k = 2.

Substitute:

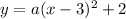
y=a(x-3)^2+2

The point (4, 6) is on athe parabola. Put the coordinates of this point to the equation:

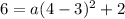6=a(4-3)^2+2 subtract 2 from both sides

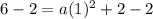
6-2=a(1)^2+2-2

$4=a\to a=4$

Finally:

y=4(x-3)^2+2 vertex form

use (a - b)² = a² - 2ab + b²

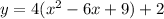y=4(x^2-6x+9)+2 use the distributive property

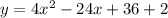
y=4x^2-24x+36+2

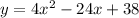y=4x^2-24x+38 standard form