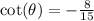Angle θ is in standard position. If (8, -15) is on the terminal ray of angle θ, find the values of the trigonometric functions.

Question

asked Mar 7, 2020 140k views

2 Answers

Eric Hauenstein · Answer 1 · 2020-03-12T06:22:38+0000

ANSWER

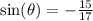
$\sin( \theta) = - (15)/(17)$

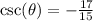
$\csc( \theta) = - (17)/(15)$

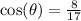
$\cos( \theta) = (8)/(17)$

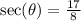
$\sec( \theta) = (17)/(8)$

$\tan( \theta) = - (15)/(8)$

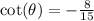
$\cot( \theta) = - (8)/(15)$

Step-by-step explanation

From the Pythagoras Theorem, the hypotenuse can be found.

${h}^(2) = 1 {5}^(2) + {8}^(2)$

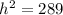
${h}^(2) = 289$

h = √(289)

h = 17

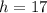
The sine ratio is negative in the fourth quadrant.

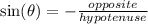
$\sin( \theta) = - (opposite)/(hypotenuse)$

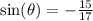
$\sin( \theta) = - (15)/(17)$

The cosecant ratio is the reciprocal of the sine ratio.

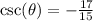
$\csc( \theta) = - (17)/(15)$

The cosine ratio is positive in the fourth quadrant.

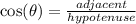
$\cos( \theta) = (adjacent)/(hypotenuse)$

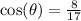
$\cos( \theta) = (8)/(17)$

The secant ratio is the reciprocal of the cosine ratio.

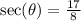
$\sec( \theta) = (17)/(8)$

The tangent ratio is negative in the fourth quadrant.

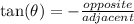
$\tan( \theta) = - (opposite)/(adjacent)$

$\tan( \theta) = - (15)/(8)$

The reciprocal of the tangent ratio is the cotangent ratio

$\cot( \theta) = - (8)/(15)$