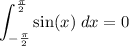Question

Interpret the following Integrals as signed areas to obtain its value​

Answer 1

Let F be the primitive of f, i.e.

`F'(x) = f`

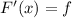
Then, we have

`\displaystyle \int_a^b f(x) = F(b)-F(a)`

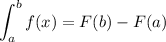
So, we have

`\displaystyle \int_0^5(2x-2)\;dx = \left[x^2-2x\right]_0^5 = 25-10=15`

As for the sine, we can spare the integral: the sine is an odd function, which means that it is symmetrical with respect to the origin. Any odd function integrated over a symmetrical neighborhood of zero (i.e. any interval of the form [-n,n]) returns zero: by symmetry, there is an equal amount of positive and negative area. So, we have

`\displaystyle \int_{-(\pi)/(2)}^{(\pi)/(2)}\sin(x)\;dx = 0`