Question

Identify an equation in slope-intercept form for thr line parallel to y=5x+2 that passes through (-6, -1).

Answer 1

Hello!

The answer is:

The equation of the line that it's parallalel to the given line and passes through the point (-6,-1) will be:

A.

`y=5x+29`

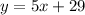
Why?

To find an equation in slope-intercept form for the linea paralallel to the given line, we must guarantee that the new line will have the same slope of the given line.

We are given the line:

`y=5x+2`

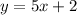
Where its slope is equal to 5

`m=5`

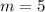
and the point (-6,-1)

The slopte-intercept form of a line, is given by the following equation:

`y=mx+b`

Then, we know that the line that we are looking for, will have a slope equal to 5, so:

`y=5x+b`

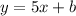
Now, substituting the given point in order to find "b", we have:

`y=5x+b`

`-1=5*(-6)+b`

`-1=-30+b`

`b=-1+30=29`

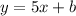
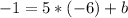
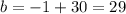
Hence, we have that the equation of the line that it's parallalel to the given line and passes through the point (-6,-1) will be:

`y=5x+29`

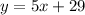
Have a nice day!

Answer 2

The correct answer option is A. y = 5x + 29.

Explanation:

We are given the following equation of a line and we are to identify the equation of a line parallel to this line which passes through (-6, -1), in slope intercept form:

`y = 5x+2`

Parallel lines have same slope, so the slope of this line will be 5.

Finding the y-intercept using the standard equation of line.

`y=mx+c`

`-1=5(-6)+c`

`c=29`

Therefore, our equation will be:

`y=5x+29`