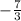Question

For the graphed exponential equation, calculate the average rate of change from x = −3 to x = 0.

graph of f of x equals 0.5 to the x power, minus 6.

Answer 1

`-(7)/(3)`

Explanation:

To solve this, we are using the average rate of change formula:

`m=(f(b)-f(a))/(b-a)`

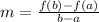
where

`m` is the average rate of change

`a` is the first point

`b` is the second point

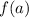`f(a)` is the function evaluated at the first point

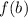`f(b)` is the function evaluated at the second point

We want to know the average rate of change of the function
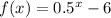`f(x)=0.5^x-6` form x = -3 to x = 0, so our first point is -3 and our second point is 0. In other words,
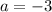`a=-3` and
`b=0`.

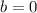Replacing values

`m=(f(b)-f(a))/(b-a)`

`m=(0.5^0-6-(0.5^(-3)-6))/(0-(-3))`

`m=(1-6-(8-6))/(3)`

`m=(-5-(2))/(3)`

`m=(-5-2)/(3)`

`m=(-7)/(3)`

`m=-(7)/(3)`

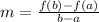
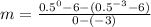
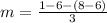
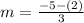
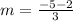
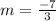
We can conclude that the average rate of change of the exponential equation form x = -3 to x = 0 is
`-(7)/(3)`