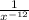Question

Can anybody please help me ?

1 The average salary for a professional baseball player in the United States can be approximated by = 283(1.2)^t where t=0 represents the year 1984. Using this approximation, find the ratio of an average salary in 1988 to the average salary in 1994.


2 Find and correct the error(s) in the problem below. Explain your correction(s).


x^-9/x^-3=x^-9-3

=x^-12

=1/x^-12

Answer 1

Here the answer is in this picture

Answer 2

1. Ratio is 1 : 3

Explanation:

1. The average salary for a professional baseball player in the United States can be approximated by =
`283(1.2)^(t)`

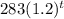
Where t = 0 represents the year 1984.

Salary in year 1988 =
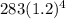`283(1.2)^(4)` [t = 4 years]

Salary in year 1994 =
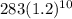`283(1.2)^(10)` [t = 10 years]

Ratio of the average salary in 1988 to the average salary in 1994 =
`(283(1.2)^(4))/(283(1.2)^(10))=((1.2)^(4))/((1.2)^(10))`

=
`(1)/((1.2)^(10-4))=(1)/((1.2)^(6))`

=
`(1)/(3)`

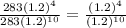
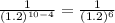
2. Corrected form

`(x^(-9) )/(x^(-3))`

=
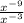
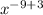`x^(-9+3)`[since
`(a^(1))/(a^(1))=a^(1-1)=a^(0)=1`]

=
`x^(-6)`

=
`(1)/(x^(6))` [ since
`(1)/(a^(1))=a^(-1)` ]

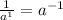Now we can compare the corrections and errors in the highlighted form.

Expression needs correction

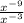
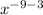
`(x^(-9) )/(x^(-3))`

=
`x^(-9-3)`

=
`x^(-12)`

=
`(1)/(x^(-12))`