Answer:
Final answer is approx 6.644 years.
Explanation:
Given that a company sold 5.75 million motorcycles and 3.5 million cars in the year 2010. The growth in the sale of motorcycles is 16% every year and that of cars is 25% every year.
So we can use growth formula:

Then we get equation for motorcycles and cars as:
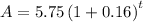
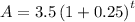
Now we need to find about when the sale of cars will be more than the sale of motorcycles. So we get:

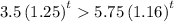
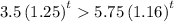
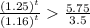
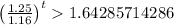
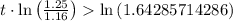

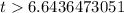
Hence final answer is approx 6.644 years.