Question

A bucket weighing 2 kg and a rope of negligible mass is used todraw water from a well that is 40.8 meters deep. Just before thebucket starts being raised from the bottom of the well, the bucket isfilled with 6 kg of water. Unfortunately, there is a hole in the bucketand water leaks out at the rate of 0.12 kg per second. The bucketis pulled up at a constant rate of 0.8 meters per second.(a)How much water is in the bucket when the bucket reaches thetop of the well?(b)Find the work done pulling the bucket to the top of the well.(Assume that the acceleration of gravity is 9.8 meters per secondper second.)

Answer 1

(a) There will be no water in the bucket by the time the bucket reaches the top of the well.

(b) The work done in this process will be approximately 1.98 × 10³ J.

Step-by-step explanation:

(a)

How long will it take for the bucket to reach the top of the well?

`\displaystyle t = (s)/(v) = \rm (40.8)/(0.8) = 51.0\;s`.

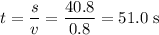How much water will leak out during that
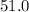`51.0` seconds?

`\rm 51.0\;s * 0.12\;kg\cdot s^(-1) = 6.12\;kg > 6\;kg`.

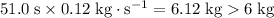That's more than all the water in the bucket. In other words, all
`\rm 6\;kg` of water in the bucket will have leaked out by the time the bucket reaches the top of the well. There will be no water in the bucket by the time the bucket reaches the top of the well.

(b)

How long will it take for all water to leak out of the bucket?

`\displaystyle \rm (6\; kg)/(0.12\;kg \cdot s^(-1)) = 50\;s`.

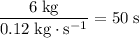In other words,

• For the first 50 seconds, water will leak out of the bucket. The mass of the bucket will decrease from
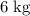  `\rm 6\;kg` to
  `\rm2\;kg` at a constant rate.
• For the last 1 second, the mass of the bucket will stay constant at
  `\rm 2\;kg`.

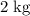Express the mass
`m` of the bucket about time
`t` as a piecewise function:

`\displaystyle m(t) = \left\{\begin{aligned} &6 - 0.12\;t,&&\;0\le t < 50\\& 2,&&\; 50\le t <51\end{aligned}`.

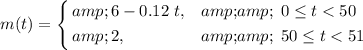Gravity on the bucket:

`W(t) = m(t)\cdot g`.

However, the bucket is moving at a constant velocity. There's no acceleration. By Newton's Second Law, the net force will be zero. Forces on the bucket are balanced. As a result, the size of the upward force shall be equal to that of gravity.

`\displaystyle F(t) = W(t) = m(t)\cdot g`.

The speed of the bucket
`v` is constant. Thus the power
`P` that pulls the bucket upward at time
`t` will be:

`P(t) = F(t)\cdot v = m(t)\cdot v\cdot g`.

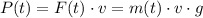Express work as a definite integral of power with respect to time:

`\displaystyle \begin{aligned}W &= \int_(t_0)^(t_1){P(t)\cdot dt} = \int_(t_0)^(t_1){m(t)\cdot g \cdot v\cdot dt}\end{aligned}`.

Both
`g` and
`v` here are constants. Factor them out:

`\displaystyle \begin{aligned}W &= \int_(t_0)^(t_1){m(t)\cdot g \cdot v\cdot dt} = v\cdot g\cdot \int_(t_0)^(t_1){m(t)\cdot dt} \end{aligned}`.

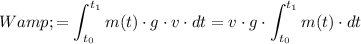Integrate the piecewise function
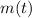`m(t)` piece-by-piece:

`\displaystyle \begin{aligned}W &= v\cdot g\cdot \int_(t_0)^(t_1){m(t)\cdot dt}\\ &=0.8* 9.8 \left [\int_(0)^(50)(8-0.12\;t)\cdot dt + \int_(50)^(51)2\cdot dt\right]\\ &=0.8* 9.8 \left [\left(8\;t - (0.12)/(2)\;t^(2)\right)\bigg|^(50)_(0) + (2\;t)\bigg|^(51)_(50)\right] \\&=0.8* 9.8 \left [\left(8* 50-(0.12)/(2)* 50^(2)\right)+ (51* 2 - 50* 2)\right]\\&=\rm 1975.68\;J \end{aligned}`.

Hence the work done pulling the bucket to the top of the well is approximately
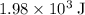`\rm 1.98* 10^(3)\;J`.