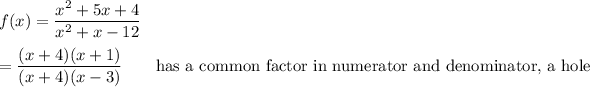Question

NEED HELP ASAP 20 PTS PLEASE.

The graph of which is the following rational functions has a hole?

Answer 1

see below

Explanation:

The denominator quadratic of each of the rational functions has two real roots, so the rational function would ordinarily have two vertical asymptotes. If there is one vertical asymptote, it is because the other one has been canceled by a numerator factor, creating a "hole."

A graph of the first rational function shows it to have only one vertical asymptote, at x=3. The product of zeros of the denominator quadratic is the constant term, -12, so the other denominator zero must be at x=-4. That is where the hole is found. (See the graph in the second attachment.)

_____

Without a graphing calculator, you would determine the zeros of each quadratic, and identify the rational function that had numerator and denominator zeros that were the same.

`f(x)=(x^2+5x+4)/(x^2+x-12)\\\\=((x+4)(x+1))/((x+4)(x-3)) \qquad\text{has a common factor in numerator and denominator, a hole}`