Question

Find the solution to the system of the equations shown below:

y = -4x + 11

y = 1/2x + 2


a.
(4, 1)
c.
(2, 3)
b.
(11, 2)
d.
(3, 2)

Answer 1

(2,3)

Explanation:

The given equations are:

`y=-4x+11`

and

`y=(1)/(2)x+2`

Equate both equations:

`(1)/(2)x+2=-4x+11`

Multiply through by 2:

`x+4=-8x+22`

`x+8x=22-4`

`9x=18`

x=2

Put x=2 into the first equation:

`y=-4(2)+11`

`y=-8+11`

y=3

The solution is (2,3)

Answer 2

C. (2, 3)

Explanation:

A system of linear equations is a set of (linear) equations that have more than one unknown. The unknowns appear in several of the equations, but not necessarily in all of them. What these equations do is relate the unknowns to each other.

Solve a system of equations is to find the value of each unknown so that all the equations of the system are met.

Ordering both equations

First equation

`y=-4y+11`

`4x+y=11`

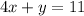
Second equation

`y=(1)/(2) x+2`

`-(1)/(2)x+y=2`

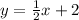
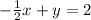
Ordering in a system of equations

`\left \{ {{4x+y=11} \atop {-(1)/(2)x+y=2}} \right.`

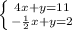
Using the reduction method which consists of operating between the equations, such as adding or subtracting both equations, so that one of the unknowns disappears. Thus, we obtain an equation with a single unknown.

We're going to subtract the second equation from the first to eliminate the unknown y.

4x + y = 11

- ((-1/2)x + y = 2)

(9/2)x = 9 ------> x= [(2)(9)]/9 -----> x = 2

Substituing the value x = 2 in
`y=(1)/(2) x+2`

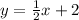
y = (1/2)x + 2 ---------> y = (1/2)(2) + 2 -------> y = (2/2) + 2

y = 1 + 2 --------> y = 3

The solution of the system of equations is (2, 3).