There are 101 athletes at a highschool. 53 of them play football, 24 play basketball, and 31 play neither sport. Find the probability of: P(Football and basketball)

Question

asked Sep 2, 2020 104k views

1 Answer

Peter Marshall · Answer 1 · 2020-09-08T14:12:26+0000

Let x represent those who both football and basketball

The given information can be illustrated in a Venn diagram as shown in the attachment.

We solve the equation below to find the value of x.

(53-x)+x+(24-x)+31=101

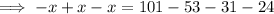
$\implies -x+x-x=101-53-31-24$

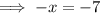
$\implies -x=-7$

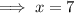
$\implies x=7$

From the second diagram;

25.
P(Basketball)=(17)/(101)

26.
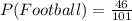
P(Football)=(46)/(101)

27.
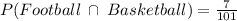$P(Football\: \cap\:Basketball)=(7)/(101)$ . This is because 7 play both Football and Basketball.

28.
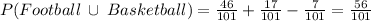$P(Football\: \cup\:Basketball)=(46)/(101)+(17)/(101)-(7)/(101)=(56)/(101)$ . This is because there is intersection.

29.
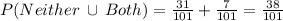$P(Neither\: \cup\:Both)=(31)/(101)+(7)/(101)=(38)/(101)$ . The two events are mutually exclusive.