Question

Graph f(x)=x2 +2x-3 label x and y intercept and vertex with their coordinates and draw axis of symmetry

Answer 1

f(x) = x² + 2x - 3 ..….equation1

The graph of function will be a parabola

Standard form of parabola:

y=ax²+bx+c

x-coordinate of the vertex can be found using

x =
`(−b)/(2a)`

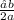
from equation 1 find values for a, b, and c.

a = 1, b = 2, c = -3 ⇒ x=−2/2(1) ⇒ x = -1

substitute the value of x into equation 1 for y-coordinate

f(-1) = (-1)² + 2(-1) – 3 ⇒ −4

vertex =(-1,−4)

Axis of symmetry = x = -1,

Axis of symmetry is vertical and passes through the vertex with equation

x = -1

For x-intercept, put y = 0

x² + 2x - 3=0 ⇒ x² + 3x -x - 3=0 ⇒ x( x + 3 ) -1 ( x + 3 ) ⇒ ( x − 1 )( x + 3 ) = 0

equate each factor to zero and solve for x

x − 1 = 0 ⇒ x = 1, x + 3 = 0 ⇒ x = -3

x-intercept = { 1, -3 }

For y-intercepts put x = 0

y = (0)² + 2(x) - 3

y = -3

y-intercept = ( 0 , -3 )

The points for the vertex, x-intercepts, and y-intercept and axis of symmetry are plotted on the graph.