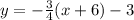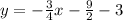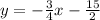Question

Use differentiation method to find the slope of the tangent hence the

equation of the tangent as shown below.
Circle with radius = 5
and centre at (-3,1)
Tagent of the
circle at x = -6

Answer 1

The equation of the tangent at x=-6 is
`y=-(3)/(4)x-(15)/(2)`

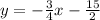
Explanation:

The equation of a circle with center (h,k) with radius r units is given by:

`(x-h)^2+(y-k)^2=r^2`

The given circle has center (-3,1) and radius 5 units.

We substitute the center and the radius into the equation to get;

`(x--3)^2+(y-1)^2=5^2`

`(x+3)^2+(y-1)^2=25`

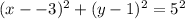
To find the slope, we differentiate implicitly to get:

`2(x+3)+2(y-1)\fra{dy}{dx}=0`

`2(y-1)(dy)/(dx)=-2(x+3)`

`(dy)/(dx)=-(x+3)/(y-1)`

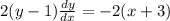
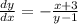
When x=-6;we have
`(-6+3)^2+(y-1)^2=25`

`\implies 9+(y-1)^2=25`

`\implies (y-1)^2=25-9`

`\implies (y-1)^2=16`

`\implies y-1=\pm √(16)`

`\implies y-1=\pm4`

`\implies y=1\pm4`

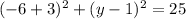
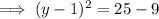
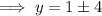
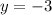`y=-3` or
`y=5`

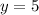
From the graph the reuired point is (-6,-3).

We substitute this point to find the slope;

`(dy)/(dx)=-(-6+3)/(-3-1)`

`(dy)/(dx)=-(3)/(4)`

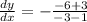
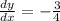
The equation is given by
`y-y_1=m(x-x_1)`.

We plug in the slope and the point to get:

`y--3=-(3)/(4)(x--6)`

`y=-(3)/(4)(x+6)-3`

`y=-(3)/(4)x-(9)/(2)-3`

`y=-(3)/(4)x-(15)/(2)`