Question

Please help!!

What is the value of x? Enter your answer in the box. x = NOTE: Image not drawn to scale. Triangle G E H with segment E D such that D is on segment G H, between G and H. Angle G E D is congruent to angle D E H. E G equals 44.8 millimeters, G D equals left parenthesis x plus 4 right parenthesis millimeters, D H equals 35 millimeters, and E H equals 56 millimeters.

Answer 1

x = 24

Explanation:

The segments on either side of an angle bisector are proportional:

(x +4)/44.8 = 35/56

x +4 = 44.8·(35/56) = 28 . . . . multiply by 44.8

x = 24 . . . . . subtract 4

Answer 2

The value of x is 24.

Explanation:

Given information: In ΔGHE, ED is angle bisector, EG=44.8 millimeters, GD=(x+4) millimeters, DH=35 millimeters, and EH=56 millimeters.

According to the angle bisector theorem, an angle bisector divide the opposite side into two segments that are proportional to the other two sides of the triangle.

In ΔGHE, ED is angle bisector, By using angle bisector theorem, we get

`(GD)/(DH)=(EG)/(EH)`

`(x+4)/(35)=(44.8)/(56)`

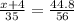
Multiply both the sides by 35.

`x+4=(44.8)/(56)* 35`

`x+4=28`

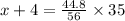
Subtract 4 from both the sides.

`x=28-4`

`x=24`

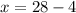
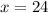
Therefore the value of x is 24.