Answer: Second Option
"the summation of 880 times one fourth to the i minus 1 power, from i equals 1 to infinity. ; the sum is 1,173"
Explanation:
We know that infinite geometrical series have the following form:
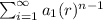
Where
 is the first term of the sequence and "r" is common ratio
is the first term of the sequence and "r" is common ratio
In this case
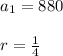
So the series is:
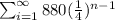
By definition if we have a geometric series of the form
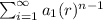
Then the series converges to
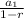 if
if

In this case
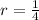 and
and
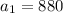 then the series converges to
then the series converges to
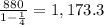
Finally the answer is the second option