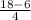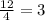Question

Given the function f(x)=-x^2+6x+13f(x)=−x

2
+6x+13, determine the average rate of change of the function over the interval -1\le x \le 5−1≤x≤5.

Answer 1

3

Explanation:

The given function is

`f(x)=-x^2+6x+13`

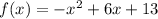
The average rate of change is simply the slope of the secant line connecting any two point on the graph of the function.

The average rate of change of this function over the interval;

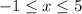`-1\le x\le 5` is given by:

`(f(5)-f(1))/(5-1)`

`f(5)=-(5)^2+6(5)+13`

`f(5)=-25+30+13=18`

`f(-1)=-(-1)^2+6(-1)+13`

`f(-1)=-1-6+13=18`

`f(-1)=6`

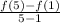
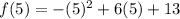
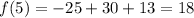
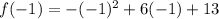
The average rate of change now becomes;

`(18-6)/(4)`

`(12)/(4)=3`