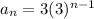Answer:
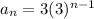
Explanation:
We have the following sequence
3,9,27,81,243
Note that if you divide each term of the sequence between the previous term you get:
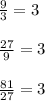
then the radius of convergence of the series is r.
therefore this is a geometrical series.
The formula to find the general term
 of the geometric sequence is:
of the geometric sequence is:
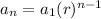
Where
 is the first term of the sequence
is the first term of the sequence
Then the general term for this sequence is: