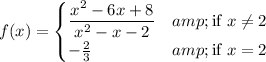Question

Write out each step of the 3-step test for continuity for the following functions at the given point. If the function is discontinuous, state the type of discontinuity

Answer 1

If we simply substitute the value x=2 in the expression we have

`f(2) = (4-12+8)/(4-2-2) = (0)/(0)`

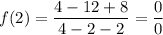
which is undefined.

But if we factor both numerator and denominator, we have

`f(x)=(x^2-6x+8)/(x^2-x-2) = ((x-2)(x-4))/((x+1)(x-2))`

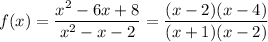
Since we are studying the limit as x approaches 2, we can assume that x is not 2. In this case, we can simplify the (x-2) parenthesis, and the expression becomes

`f(x)=(x-4)/(x+1)`

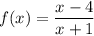
And we can evaluate this at 2 with no problems:

`f(2) = (2-4)/(2+1) = -(2)/(3)`

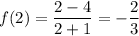
So, we have

`\displaystyle \lim_(x\to 2)f(x) = -(2)/(3)`

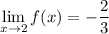
This means that in this case both left and right limits exist and are the same, so the limit exists, but the function is not defined at x=2. This is a removable discontinuity, because we can define the function as its limit, and we have a continuous function at x=2:

`f(x) = \begin{cases}(x^2-6x+8)/(x^2-x-2) &\text{if }x \\eq 2\\ -(2)/(3) &\text{if }x = 2\end{cases}`