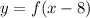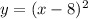Which function represents a translation of the graph of y = x^2 by 8 units to the right? A. y=x^2+8 B. y=8x^2 C. y=(x-8)^2 D. y=(x+8)^2

Question

Which function represents a translation of the graph of y = x^2 by 8 units to the right?

A.
`y=x^2+8`
B.
`y=8x^2`
C.
`y=(x-8)^2`
D.
`y=(x+8)^2`

Answer 1

Option C.
`y = (x-8) ^ 2`

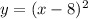
Explanation:

If we have a parent function f(x) and we want to make a transformation that translates the graph of f(x) horizontally then we do

`y = f (x + h)`

Where h is a constant such that:

If
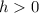`h> 0` then the graph of f(x) moves h units to the left

If
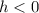`h <0` then the graph of f(x) moves h units to the right.

In this case we have the function
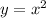`y = x ^ 2` and we know that 8 units are moved to the right. If you move 8 units to the right This means that

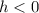`h <0` and
`h = -8`

So if
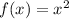`f(x) = x ^ 2` the transformed function will be:

`y = f(x -8)`

`y = (x-8) ^ 2`