Question

At 2:45 p.m., a jet is located 56 mi due east of a city. A second jet is located 30 mi due north of the city. To the nearest tenth of a mile, what is the distance between the two jets?

Answer 1

the answer is 63.5 mi.

Explanation:

Answer 2

Hello!

The answer is:

The distance between the two jets is 63.5 mi.

Why?

From the statement we know that the first jet is located 56 mi due to the east city while the second jet is located 30 mi due to the north, so, we can calculate the distance between the two jets using the Pythagorean Theorem.

The Pythagorean Theorem states that:

`c^(2)=a^(2) +b^(2)`

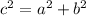
So,

`Distance=\sqrt{(Jet_(1)Location)^(2)+(Jet_(2)Location)^(2)}\\\\Distance=\sqrt{(56mi)^(2)+(30mi)^(2)}=\sqrt{3136mi^(2)+900mi^(2)} \\\\Distance=\sqrt{3136mi^(2)+900mi^(2)}=\sqrt{4036mi^(2)}=63.5mi`

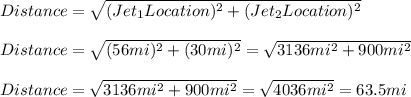
Hence, the distance between the two jets is 63.5 mi.

Have a nice day!