Question

Five cards are dealt from 52.

A) How many different hands can be dealt?
B) How many hands will contain 4 hearts?
C) How many hands will contain no face cards?
D) How many hands will contain only spades or only clubs?
E) How many hands will contain only red cards l?
F) How many hands will contain no more than 2 face cards?
G) How many will contain at least 2 hearts?

Answer 1

For reference,

`\dbinom nk=(n!)/(k!(n-k)!)`

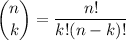
a.
`\dbinom{52}5=2,598,960` - nothing special here, you're just choosing any 5 cards from the deck

b.
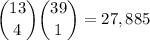`\dbinom{13}4\dbinom{39}1=27,885` - 13 hearts to choose from, and 39 of any other suit

c.
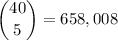`\dbinom{40}5=658,008` - there are 12 face cards to omit from the count

d.
`\dbinom{26}5=65,780` - half the deck contains spades/clubs

e.
`\dbinom{26}5=65,780` - essentially the same situtation as (d)

f.
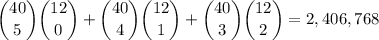`\dbinom{40}5\dbinom{12}0+\dbinom{40}4\dbinom{12}1+\dbinom{40}3\dbinom{12}2=2,406,768` - either 0, 1, or 2 face cards are allowed

g.
`\dbinom{13}2\dbinom{39}3+\dbinom{13}3\dbinom{39}2+\dbinom{13}4\dbinom{39}1+\dbinom{13}5\dbinom{39}0=953,940` - similar to (f)