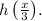The correct answer to the question is option (2):
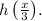
To address the question about the horizontal stretching of the graph of a function
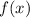 by a factor of 3, we need to understand how transformations affect the graph of a function. Here are the steps to determine the correct transformation:
by a factor of 3, we need to understand how transformations affect the graph of a function. Here are the steps to determine the correct transformation:
1. Identify the Base Function: Recognize that the graph in question is of some function
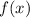 . We don't need to know the form of \( f(x) \) to understand how it will be transformed.
. We don't need to know the form of \( f(x) \) to understand how it will be transformed.
2. Understand Horizontal Stretching: A horizontal stretch by a factor of
 is achieved by replacing every
is achieved by replacing every
 in the function with
in the function with
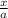 . In this case,
. In this case,
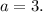
3. Apply the Stretch to the Function: Replace
 with
with
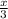 in the function
in the function
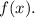
4. **Write Down the Transformed Function**: The new function after the horizontal stretch will be

5. **Choose the Correct Answer**: Look for the choice that represents the transformation

The correct transformation that indicates a horizontal stretch by a factor of 3 is:
![\[ f\left((x)/(3)\right) \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/s94hrvu98lmb0kj3q42hzismtvw2vlqgr3.png)
This means that for any given value of
 in the original function, its corresponding point on the graph will now be three times further away from the y-axis, thus stretching the graph horizontally. If the original function had a point at
in the original function, its corresponding point on the graph will now be three times further away from the y-axis, thus stretching the graph horizontally. If the original function had a point at
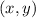 , the new function after the stretch will have a corresponding point at
, the new function after the stretch will have a corresponding point at
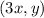 , which means the x-values have been stretched out.
, which means the x-values have been stretched out.
Now, from the options given in the image:
1.
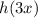 represents a horizontal compression by a factor of 3, not a stretch.
represents a horizontal compression by a factor of 3, not a stretch.
2.
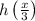 is the correct representation of a horizontal stretch by a factor of 3.
is the correct representation of a horizontal stretch by a factor of 3.
3.
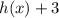 represents a vertical shift upwards by 3 units.
represents a vertical shift upwards by 3 units.
4.
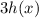 represents a vertical stretch by a factor of 3.
represents a vertical stretch by a factor of 3.
Therefore, the correct answer to the question is option (2):