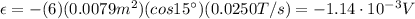Question

A metal detector uses a changing magnetic field to detect metallic objects. Suppose a metal detector that generates a uniform magnetic field perpendicular to its surface is held stationary at an angle of 15.0∘ to the ground, while just below the surface there lies a silver bracelet consisting of 6 circular loops of radius 5.00 cm with the plane of the loops parallel to the ground. If the magnetic field increases at a constant rate of 0.0250 T/s, what is the induced emf E? Take the magnetic flux through an area to be positive when B⃗ crosses the area from top to bottom.

Answer 1

Induced emf,
`\epsilon=-1.13* 10^(-3)\ volts`

Step-by-step explanation:

It is given that,

Number of circular loop, N = 6

A uniform magnetic field perpendicular to its surface is held stationary at an angle of 15 degrees to the ground.

Radius of the loop, r = 5 cm = 0.05 m

Change in magnetic field,
`(dB)/(dt)=0.025\ T/s`

Due to the change in magnetic field, an emf will be induced. Let E is the induced emf in the coil. it is given by :

`\epsilon=(d\phi)/(dt)`

`\phi` = magnetic flux

`\epsilon=(d(NBA\ cos\theta))/(dt)`

`\epsilon=-NA(d(B))/(dt)`

`\epsilon=6* \pi (0.05)^2* 0.025* cos(15)`

`\epsilon=-1.13* 10^(-3)\ volts`

So, the induced emf in the loop is
`1.13* 10^(-3)\ volts` . Hence, this is the required solution.

Answer 2

`-1.14 \cdot 10^(-3) V`

Step-by-step explanation:

The induced emf in the loop is given by Faraday's Newmann Lenz law:

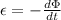`\epsilon = - (d \Phi)/(dt)` (1)

where

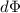`d\Phi` is the variation of magnetic flux

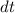`dt` is the variation of time

The magnetic flux through the coil is given by

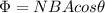`\Phi = NBA cos \theta` (2)

where

N = 6 is the number of loops

A is the area of each loop

B is the magnetic field strength

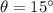`\theta =15^(\circ)` is the angle between the direction of the magnetic field and the normal to the area of the coil

Since the radius of each loop is r = 5.00 cm = 0.05 m, the area is

`A=\pi r^2 = \pi (0.05 m)^2=0.0079 m^2`

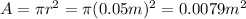
Substituting (2) into (1), we find

`\epsilon = - (d (NBA cos \theta))/(dt)= -(NAcos \theta) (dB)/(dt)`

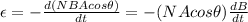
where

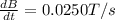`(dB)/(dt)=0.0250 T/s` is the rate of variation of the magnetic field

Substituting numbers into the last formula, we find

`\epsilon = -(6)(0.0079 m^2)(cos 15^(\circ))(0.0250 T/s)=-1.14 \cdot 10^(-3) V`