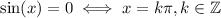None of these. All of these functions are defined as ratio of trigonometric functions.
Trigonometric functions have infinite zeroes, so when you put them in the denominator, they lead to infinitely many points of ill-definition.
Specifically, we have:

which is undefined at
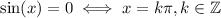
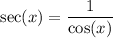
which is undefined at
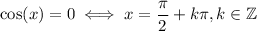
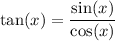
which is undefined at
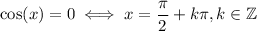
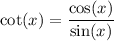
which is undefined at