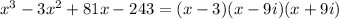Question

how can I rewrite x^3-3x^2+81x-243 in the form of (x-d)(x-e)(x+f) where d is a real number and e and f are complex numbers of the form bi?

Answer 1

If
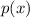`p(x)` is a polynomial of degree
`N` and
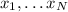`x_1,\ldots x_N` are his roots, we can write

`p(x)=(x-x_1)(x-x_2)\ldots(x-x_N)`

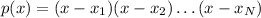
So, the exercise is basically asking you to find the three roots of the polynomial.

Cubic polynomials don't have a closed formula to solve them (well, they have, but it's very complicated), so we'd better use the rational root theorem.

This theorem states that the possible rational solutions of a polynomial with integer coefficients are of the form
`(p)/(q)`, where p is a divisor of the known term, and q is a divisor of the leading term.

So, in our case, we have to try all the divisors of 243 (with both signs). We find out that

`p(3) = 0`

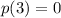
So, x=3 is a solutions, and we can write as

`p(x) = (x-3)r(x)`

And we can find the remaining polynomial by writing

`r(x) = (p(x))/(x-3) = x^2+81`

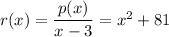
The solutions of this polynomial are

`x^2+81 = 0 \iff x^2=-81 \iff x = \pm 9i`

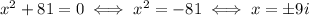
This means that the solutions of
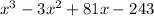`x^3-3x^2+81x-243` are
`x=3`,
`x=9i`,
`x=-9i`

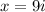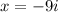
So, we can factor it as

`x^3-3x^2+81x-243=(x-3)(x-9i)(x+9i)`