What is the length of the conjugate axis? ((x-2)^2)/(36) - ((y+1)^2)/(64) =1

Question

What is the length of the conjugate axis?


`((x-2)^2)/(36) - ((y+1)^2)/(64) =1`

Answer 1

the length of the conjugate axis is 16

Explanation:

We know that the general equation of a hyperbola with transverse horizontal axis has the form:

`((x-h)^2)/(a^2) - ((y-k)^2)/(b^2) = 1`

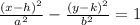
Where the point (h, k) are the coordinates of the center of the ellipse

2a is the length of the transverse horizontal axis

2b is the length of the conjugate axis

In this case the equation of the ellipse is:

`((x-2)^2)/(36) + ((y+1)^2)/(64) = 1`

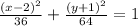
Then

`b^2 = 64\\\\b = √(64)\\\\b = 8\\\\2b = 16`

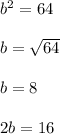
Finally the length of the conjugate axis is 16