Answer:

Explanation:
The rational roots theorem tells you that given a polynomial function with integer or whole number coefficients, a list of possible solutions can be found by listing the factors of the constant, or last term, over the factors of the coefficient of the leading term.
In your case, for the polynomial

- the last term is 20;
- the leading coeeficient is 3.
So, possible rational roots can be among:
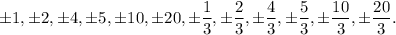
Note that
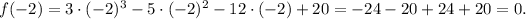
This means that
 is a root of the polynomial and
is a root of the polynomial and
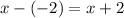 is the factor. Also
is the factor. Also
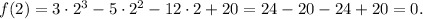
This means that
 is a root of the polynomial and
is a root of the polynomial and
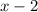 is the factor. Also
is the factor. Also
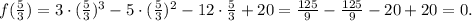
This means that
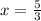 is a root of the polynomial and
is a root of the polynomial and
 is the factor.
is the factor.
Then
